题解 [宛若青空]
题目大意
给出 $n$ 个站台的人数 $a_i$ 和坐标 $d_i$,每次对区间 $[l,r]$ 询问 $\min\limits_{k=l}^r\{\,\sum\limits_{i=l}^{r}a_i|d_i-d_k|\,\}$,要求支持对人数 $a_i$ 进行区间加。
思路
Sol 1(Subtask 1)
直接暴力,对于询问暴力枚举站台 $k$,求区间内其他站台的人到站台 $k$ 的代价和,修改操作直接暴力修改。
时间复杂度:$O(qn^2)$。
期望得分:10 pts。
Sol 2(Subtask 2)
设询问区间 $[l,r]$,选定站台 $k$,最终代价为
$$ \begin{aligned} C(l,r,k)&=\sum_{i=l}^{k}a_i(d_i-d_k)+\sum_{i=k+1}^ra_i(d_k-d_i) \\ &=\sum_{i=l}^{k}a_id_i-\sum_{i=k+1}^{r}a_id_i-d_k\sum_{i=l}^k a_i+d_k\sum_{i=k+1}^{r}a_i \end{aligned} $$设 $f_i=\sum_{k=1}^i a_i$,$g_i=\sum_{k=1}^i a_i d_i$,则原式为
$$ C(l,r,k)=(g_k-g_{l-1})-(g_r-g_k)-(f_k-f_{l-1})+(f_r-f_k) $$于是似乎就可以暴力枚举选择哪个点,然后 $O(1)$ 计算答案了?
别急,注意到这样可能会爆 long long,我们需要继续找性质。
不难发现一个站台左边的人数和与右边的人数和之差最小时,那么一定选这个站台。换句话说,从左到右考虑站台 $k$, 第一个满足 $\sum_{i=l}^k a_i \ge \sum_{i=k+1}^r a_i$ 的站台就是我们要的站台。
为什么呢?考虑 $a_i\le1$ 的情况,画出图来长这样:
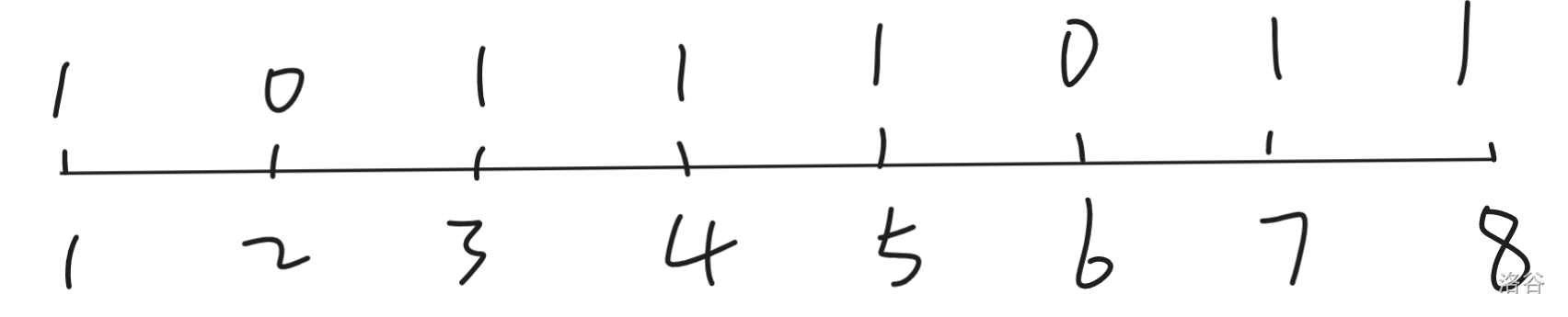
下面的数表示站台编号,上面的数表示 $a_i$。
当站在站台 $4$ 和站台 $5$ 之间时,每往左走一小点左边减小的代价和右边增大的代价是一样的,因为左边的人数等于右边的人数。
而当站在站台 $4$ 往站台 $3$ 走时,右边增大的代价大于左边减小的代价。因此第一个左边(包含自己)的人数和大于等于右边(不包含自己)的人数和的站台,一定是代价和最小的站台。
对于 $a_i>1$ 的情况也是完全一样的。
因此,只需要从左往右扫,找到第一个 $f_k-f_{l-1}\ge f_r-f_{k}$ 的位置 $k$,$C(l,r,k)$ 即为所求答案。
然后每次修改的时候除了改 $a_i$ 还要 $O(n)$ 算一遍 $f_i$ 和 $g_i$。
时间复杂度:$O(qn)$。
期望得分:40 pts。
Sol 3(Subtask 3)
这个点是留给分块的,维护一下每个块的 $a_i$ 与 $a_id_i $ 和,询问从左到右扫每个块(两边的散块暴力扫),然后找到第一个左边的 $a_i$ 和大于右边的 $a_i$ 和的块,再在块内扫,最终求出答案。
对于修改,散块直接暴力修改,整块打上懒标记即可。
时间复杂度:$O(n+q\sqrt n)$。(其实用 Sol 4 的优化可以将询问优化成 $O(\log n)$)
期望得分:60 pts。
没有代码(懒得写了)。
Sol 4(Subtask 4)
不超过 10 次修改,意味着可以暴力修改,考虑优化查询。
发现要找第一个满足 $f_k-f_{l-1}\ge f_r-f_{k}$ 的位置可以二分,因为满足这个条件的位置只有右边这一半区间,二分找到那个分界点即可。
设询问数为 $q_1$,修改数为 $q_2$,则时间复杂度:$O(q_1\log n+q_2 n)$
至此,期望得分:70 pts。
Sol 5 (Subtask 5)
不超过 10 次询问,意味着需要优化修改,发现 $f_i=\sum_{k=1}^i a_i$ 与 $g_i=\sum_{k=1}^i a_i d_i$ 其实可以用线段树维护,记 $F_x,G_x,D_i$ 分别为线段树上 $x$ 结点区间的 $a_i,a_id_i,d_i$ 和,$len_x$ 为 $x$ 结点维护区间的长度。
对于区间加 $v$,直接打上区间懒标记,并且令
$$ F_x\leftarrow F_x+len_x\times v $$ $$ G_x\leftarrow G_x+D_x\times v$$询问时直接区间查询(在 Sol 2 基础上)。
时间复杂度:$O(n+q_1\log n+q_2\log n)$
带上上面的,期望得分:80 pts。
Sol 6(Subtask 6)
(这个特殊性质其实没什么用)
发现 Sol 4 和 Sol 5 其实可以合并,即用线段树维护区间和,然后查询的时候二分。
但这样做查询是 $O(\log^2n)$ 的,并不能过掉最后一个 Subtask。
时间复杂度:$O(n+q\log^2n)$。
期望得分:90 pts。
Sol 7(正解)
注意到没有必要在外面进行二分,可以直接在线段树上二分,每次 $[l,mid]$ 的 $a_i$ 和不小于 $[mid+1,r]$ 的,就往左找,否则往右找(这里的 $l$ 和 $r$ 指的是询问中的)。
但询问是个区间,向下递归时只能维护 $[1,mid]$ 与 $[mid+1,r]$ 的 $a_i$ 和,所以在找之前还需要查询区间 $[1,l-1]$ 和 $[r+1,n]$ 的 $a_i$ 和,找的时候减一下即可。
时间复杂度:$O(n+q\log n)$。
期望得分:100 pts。
ps:这种区间操作用文艺平衡树也能做,还能支持插入,翻转区间,复制区间等神奇操作。
暂无评论,快来抢沙发!